What is an adversarial attack in NLP?
This documentation page was adapted from a blog post we wrote about adversarial examples in NLP.
This page is intended to clear up some terminology for those unclear on the meaning of the term ‘adversarial attack’ in natural language processing. We’ll try and give an intro to NLP adversarial attacks, try to clear up lots of the scholarly jargon, and give a high-level overview of the uses of TextAttack.
This article talks about the concept of adversarial examples as applied to NLP (natural language processing). The terminology can be confusing at times, so we’ll begin with an overview of the language used to talk about adversarial examples and adversarial attacks. Then, we’ll talk about TextAttack, an open-source Python library for adversarial examples, data augmentation, and adversarial training in NLP that’s changing the way people research the robustness of NLP models. We’ll conclude with some thoughts on the future of this area of research.
An adversarial example is an input designed to fool a machine learning model [1]. In TextAttack, we are concerned with adversarial perturbations, changes to benign inputs that cause them to be misclassified by models. ‘Adversarial perturbation’ is more specific than just ‘adversarial example’, as the class of all adversarial examples also includes inputs designed from scratch to fool machine learning models. TextAttack attacks generate a specific kind of adversarial examples, adversarial perturbations.
As alluded to above, an adversarial attack on a machine learning model is a process for generating adversarial perturbations. TextAttack attacks iterate through a dataset (list of inputs to a model), and for each correctly predicted sample, search for an adversarial perturbation (we’ll talk more about this later). If an example is incorrectly predicted to begin with, it is not attacked, since the input already fools the model. TextAttack breaks the attack process up into stages, and provides a system of interchangeable components for managing each stage of the attack.
Adversarial robustness is a measurement of a model’s susceptibility to adversarial examples. TextAttack often measures robustness using attack success rate, the percentage of attack attempts that produce successful adversarial examples, or after-attack accuracy, the percentage of inputs that are both correctly classified and unsuccessfully attacked.
To improve our numeracy when talking about adversarial attacks, let’s take a look at a concrete example of some attack results:

These results come from using TextAttack to run the DeepWordBug attack on an LSTM trained on the Rotten Tomatoes Movie Review sentiment classification dataset, using 200 total examples. These results come from using TextAttack to run the DeepWordBug attack on an LSTM trained on the Rotten Tomatoes Movie Review sentiment classification dataset, using 200 total examples.
This attack was run on 200 examples. Out of those 200, the model initially predicted 43 of them incorrectly; this leads to an accuracy of 157/200 or 78.5%. TextAttack ran the adversarial attack process on the remaining 157 examples to try to find a valid adversarial perturbation for each one. Out of those 157, 29 attacks failed, leading to a success rate of 128/157 or 81.5%. Another way to articulate this is that the model correctly predicted and resisted attacks for 29 out of 200 total samples, leading to an accuracy under attack (or “after-attack accuracy”) of 29/200 or 14.5%.
TextAttack also logged some other helpful statistics for this attack. Among the 157 successful attacks, on average, the attack changed 15.5% of words to alter the prediction, and made 32.7 queries to find a successful perturbation. Across all 200 inputs, the average number of words was 18.97.
Now that we have provided some terminology, let’s look at some concrete examples of proposed adversarial attacks. We will give some background on adversarial attacks in other domains and then examples of different attacks in NLP.
Terminology
Research in 2013 [2] showed neural networks are vulnerable to adversarial examples. These original adversarial attacks apply a small, well-chosen perturbation to an image to fool an image classifier. In this example, the classifier correctly predicts the original image to be a pig. After a small perturbation, however, the classifier predicts the pig to be an airliner (with extremely high confidence!).
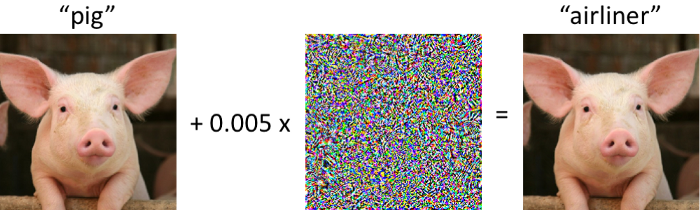
An adversarial example for an ImageNet classifier. Superimposing a tiny (but deliberate) amount of noise causes the model to classify this pig as an airliner.
These adversarial examples exhibit a serious security flaw in deep neural networks. Therefore adversarial examples pose a security problem for downstream systems that include neural networks, including text-to-speech systems and self-driving cars. Adversarial examples are useful outside of security: researchers have used adversarial examples to improve and interpret deep learning models.
As you might imagine, adversarial examples in deep neural networks have caught the attention of many researchers around the world, and this 2013 paper spawned an explosion of research into the topic.
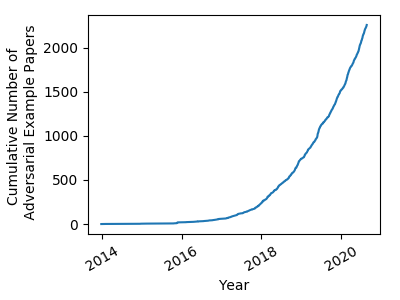
The number of papers related to ‘adversarial examples’ on arxiv.org between 2014 and 2020. [Graph from https://nicholas.carlini.com/writing/2019/all-adversarial-example-papers.html]
Many new, more sophisticated adversarial attacks have been proposed, along with “defenses,” procedures for training neural networks that are resistant (“robust”) against adversarial attacks. Training deep neural networks that are highly accurate while remaining robust to adversarial attacks remains an open problem [3].
Naturally, many have wondered about what adversarial examples for NLP models might be. No natural analogy to the adversarial examples in computer vision (like the pig-to-airliner bamboozle above) exists for NLP. After all, two sequences of text cannot be truly indistinguishable without being the same. (In the above example, the pig-classified input and its airliner-classified perturbation are literally indistinguishable to the human eye.)
Adversarial Examples in NLP

Two different ideas of adversarial examples in NLP. These results were generated using TextAttack on an LSTM trained on the Rotten Tomatoes Movie Review sentiment classification dataset. These are real adversarial examples, generated using the DeepWordBug and TextFooler attacks. To generate them yourself, after installing TextAttack, run ‘textattack attack — model lstm-mr — num-examples 1 — recipe RECIPE — num-examples-offset 19’ where RECIPE is ‘deepwordbug’ or ‘textfooler’.
Because two text sequences are never indistinguishable, researchers have proposed various alternative definitions for adversarial examples in NLP. We find it useful to group adversarial attacks based on their chosen definitions of adversarial examples.
Although attacks in NLP cannot find an adversarial perturbation that is literally indistinguishable to the original input, they can find a perturbation that is very similar. Our mental model groups NLP adversarial attacks into two groups, based on their notions of ‘similarity’:
Visual similarity. Some NLP attacks consider an adversarial example to be a text sequence that looks very similar to the original input – perhaps just a few character changes away – but receives a different prediction from the model. Some of these adversarial attacks try to change as few characters as possible to change the model’s prediction; others try to introduce realistic ‘typos’ similar to those that humans would make.
Some researchers have raised concern that these attacks can be defended against quite effectively, either by using a rule-based spellchecker or a sequence-to-sequence model trained to correct adversarial typos. TextAttack attack recipes that fall under this category: deepwordbug, hotflip, pruthi, textbugger*, morpheus
Semantic similarity. Other NLP attacks consider an adversarial example valid if it is semantically indistinguishable from the original input. In other words, if the perturbation is a paraphrase of the original input, but the input and perturbation receive different predictions, then the input is a valid adversarial example.
Some NLP models are trained to measure semantic similarity. Adversarial attacks based on the notion of semantic indistinguishability typically use another NLP model to enforce that perturbations are grammatically valid and semantically similar to the original input.
TextAttack attack recipes that fall under this category: alzantot, bae, bert-attack, faster-alzantot, iga, kuleshov, pso, pwws, textbugger*, textfooler
*The textbugger attack generates perturbations using both typo-like character edits and synonym substitutions. It could be considered to use both definitions of indistinguishability.
Generating adversarial examples with TextAttack
TextAttack supports adversarial attacks based in both definitions of indistinguishability. Both types of attacks are useful for training more robust NLP models. Our goal is to enable research into adversarial examples in NLP by providing a set of intuitive, reusable components for building as many attacks from the literature as possible.
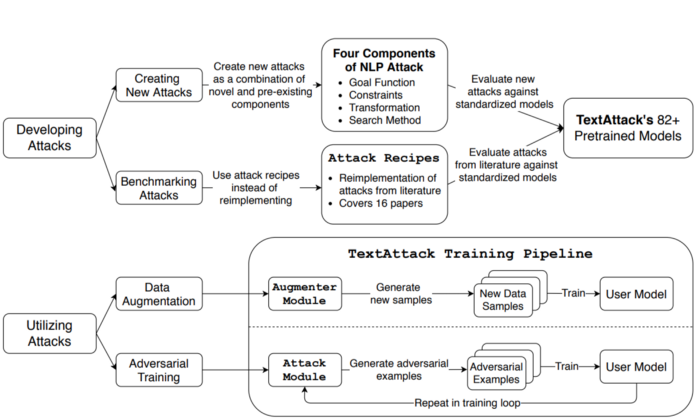
We define the adversarial attack processing using four components: a goal function, constraints, transformation, and search method. (We’ll go into this in detail in a future post!) These components allow us to reuse many things between attacks from different research papers. They also make it easy to develop methods for NLP data augmentation.
TextAttack also includes code for loading popular NLP datasets and training models on them. By integrating this training code with adversarial attacks and data augmentation techniques, TextAttack provides an environment for researchers to test adversarial training in many different scenarios.
The following figure shows an overview of the main functionality of TextAttack:
The future of adversarial attacks in NLP
We are excited to see the impact that TextAttack has on the NLP research community! One thing we would like to see research in is the combination of components from various papers. TextAttack makes it easy to run ablation studies to compare the effects of swapping out, say, search method from paper A with the search method from paper B, without making any other changes. (And these tests can be run across dozens of pre-trained models and datasets with no downloads!)
We hope that use of TextAttack leads to more diversity in adversarial attacks. One thing that all current adversarial attacks have in common is that they make substitutions on the word or character level. We hope that future adversarial attacks in NLP can broaden scope to try different approaches to phrase-level replacements as well as full-sentence paraphrases. Additionally, there has been a focus on English in the adversarial attack literature; we look forward to seeing adversarial attacks applied to more languages.
To get started with TextAttack, you might want to start with one of our introductory tutorials.
.. [1] “Attacking Machine Learning with Adversarial Examples”, Goodfellow, 2013. [https://openai.com/blog/adversarial-example-research/]
.. [2] “Intriguing properties of neural networks”, Szegedy, 2013. [https://arxiv.org/abs/1312.6199]
.. [3] “Robustness May Be at Odds with Accuracy”, Tsipras, 2018. [https://arxiv.org/abs/1805.12152]